「方程式」と言ってもいろいろありますが、この記事では、中学1年生で習う「一次方程式」を基本から解き方のコツまでわかりやすく解説していきます。
これが全ての方程式の基礎にもなるのでしっかり押さえておきましょう。
中学生の方も、大人の学び直しの方もどなたでもご覧ください。
一次方程式とは?
一次方程式とは、文字(xなど)を使った、次数が1の方程式のことです。
「次数」に関しては中学2年生で勉強するのでここでは、
「文字(xなど)を使った式のことを方程式と呼ぶ」
と理解しておいて大丈夫です。
で、どのような式なのか?
例えば、

このような式で、「xにどんな数を入れたら右と左が同じになるか」を求めるものが
方程式の解を求める問題です。
xの中に入る数を当てるゲームだと考えるとわかりやすいと思います。
方程式の解き方
では、どのように解いていくのでしょうか?
xに当てはまる数を考えるので、一つずつ当てはめていく方法もありますが、答えは分数になる可能性も考えると候補が多すぎて全て当てはめて考えることは不可能です。
そこで、「移項」と「逆数をかける」という方法を使ってxを求めていきます。
移項
移項とは項を「=」を飛び越えて移動させることです。
方程式の目的はxにどのような数字が入るか求めること、つまり
x=⚪︎⚪︎
の形を作ることです。
この形を作るために移項を利用します。
移行させる時には符号(+, −)が変わります。ここはミスも多いので注意しましょう。
では、例題を見てみましょう。
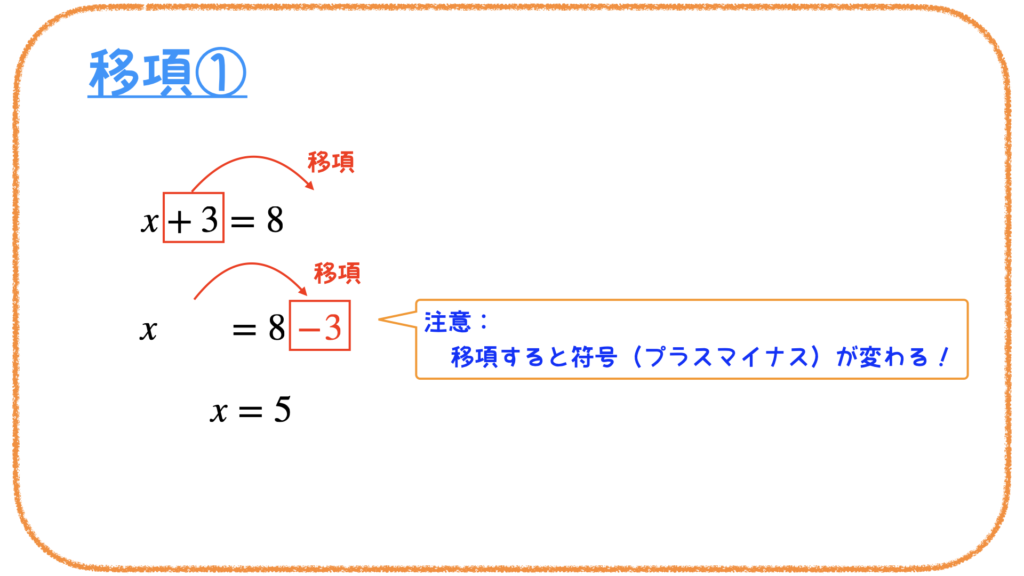
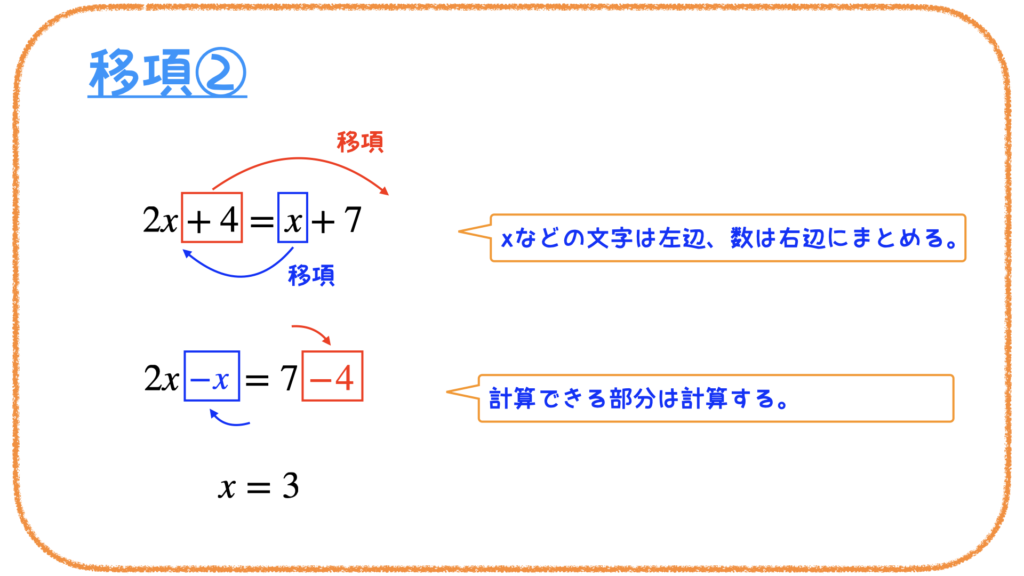
このように「x=」の形を作るために、
xは=の左側(左辺)、
その他は=の右側(右辺)に移動させます。

でも、勝手に移動しちゃっていいの?

移動して良いと覚えてしまってOK!
でも実はこれ、移動しているわけではなく、数学の決まりに従って変形した結果、
移動しているように見えるだけなんだ。
その辺の詳しい説明も記事を準備するので気になる場合は読んでみてね。
逆数をかける
では次のような問題の場合はどうでしょうか?

移項を使っても「x=」の形になりません。
xにくっついている数(「係数」といいます)は移項できません。
そこで係数の逆数をかけます。
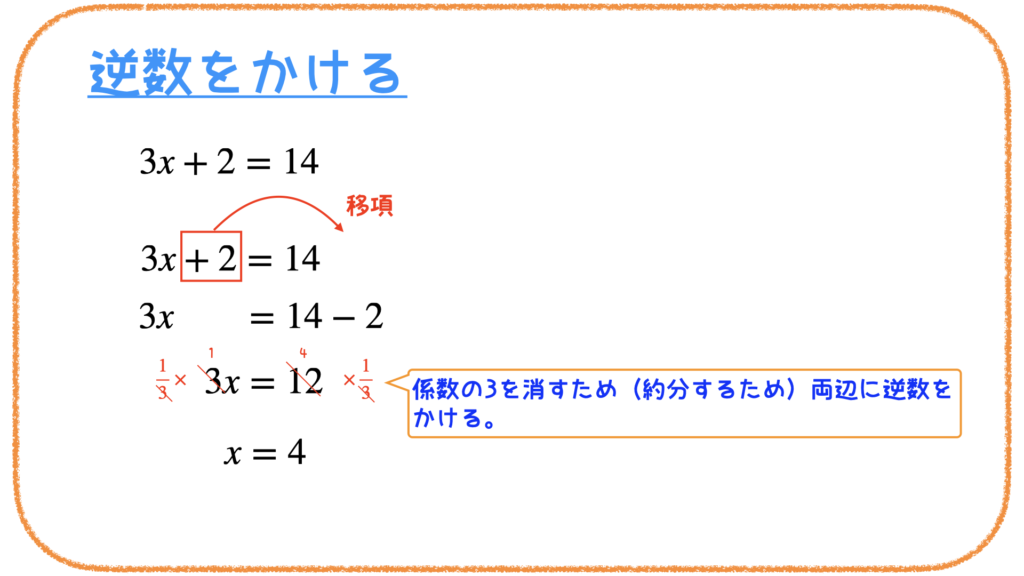
これで、「x=」の形になってxを求めることができました。
まとめ

方程式のゴールとなる形は「x = ⚪︎」なので、左側(左辺)が x のみにならなければなりません。
そのために移項や逆数をかけるという手段を使うという感覚です。
最初は解くのに時間もかかるかもしれませんが、練習で数をこなすことで慣れてきます。
練習問題もいくつか用意してますので練習してみましょう。
練習問題
問題

解答

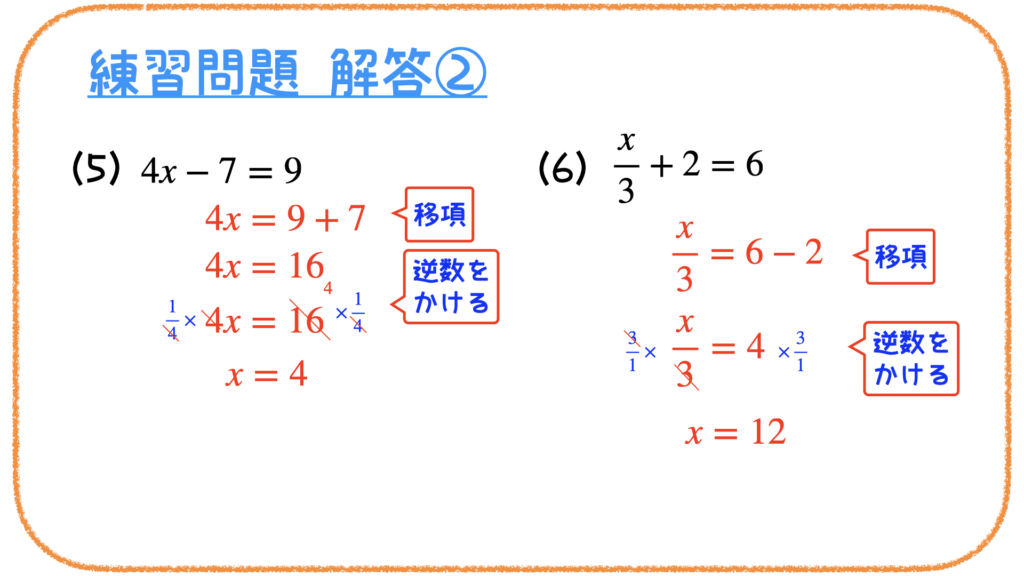



コメント